Symmetric Ciphers1
第三章好像是做的最迷的
虽然只需要做 ”How AES Works” 部分。但是——
刚开始第三章:还以为会越来越难,没想到做完数论就柳暗花明了?
第三章最后一题:什么东西啊这是,这怎么比数论那块还复杂。。
How AES Works
Keyed Permutations
Description
AES, like all good block ciphers, performs a “keyed permutation”. This means that it maps every possible input block to a unique output block, with a key determining which permutation to perform.
A “block” just refers to a fixed number of bits or bytes, which may represent any kind of data. AES processes a block and outputs another block. We’ll be specifically talking the variant of AES which works on 128 bit (16 byte) blocks and a 128 bit key, known as AES-128.
Using the same key, the permutation can be performed in reverse, mapping the output block back to the original input block. It is important that there is a one-to-one correspondence between input and output blocks, otherwise we wouldn’t be able to rely on the ciphertext to decrypt back to the same plaintext we started with.
What is the mathematical term for a one-to-one correspondence?
Analyze
喔这题简单,我不知道但 Google 知道,浅搜一下”一一对应的数学术语“,知道叫双射函数,浅浅上个百科,就知道英语咯。
Resisting Bruteforce
Description
If a block cipher is secure, there should be no way for an attacker to distinguish the output of AES from a random permutation of bits. Furthermore, there should be no better way to undo the permutation than simply bruteforcing every possible key. That’s why academics consider a cipher theoretically “broken” if they can find an attack that takes fewer steps to perform than bruteforcing the key, even if that attack is practically infeasible.
How difficult is it to bruteforce a 128-bit keyspace? Somebody estimated that if you turned the power of the entire Bitcoin mining network against an AES-128 key, it would take over a hundred times the age of the universe to crack the key.
It turns out that there is an attack on AES that’s better than bruteforce, but only slightly – it lowers the security level of AES-128 down to 126.1 bits, and hasn’t been improved on for over 8 years. Given the large “security margin” provided by 128 bits, and the lack of improvements despite extensive study, it’s not considered a credible risk to the security of AES. But yes, in a very narrow sense, it “breaks” AES.
Finally, while quantum computers have the potential to completely break popular public-key cryptosystems like RSA via Shor’s algorithm, they are thought to only cut in half the security level of symmetric cryptosystems via Grover’s algorithm. This is one reason why people recommend using AES-256, despite it being less performant, as it would still provide a very adequate 128 bits of security in a quantum future.
What is the name for the best single-key attack against AES?
Analyze
虽然但是,依然去查了 Google,靠谱!
不过发现网上搜 biclique 的结果居然不是很多,我打开方式有问题吗是,后面再看看。
Structure of AES
Description
To achieve a keyed permutation that is infeasible to invert without the key, AES applies a large number of ad-hoc mixing operations on the input. This is in stark contrast to public-key cryptosystems like RSA, which are based on elegant individual mathematical problems. AES is much less elegant, but it’s very fast.
At a high level, AES-128 begins with a “key schedule” and then runs 10 rounds over a state. The starting state is just the plaintext block that we want to encrypt, represented as a 4x4 matrix of bytes. Over the course of the 10 rounds, the state is repeatedly modified by a number of invertible transformations.
Each transformation step has a defined purpose based on theoretical properties of secure ciphers established by Claude Shannon in the 1940s. We’ll look closer at each of these in the following challenges.
Here’s an overview of the phases of AES encryption:
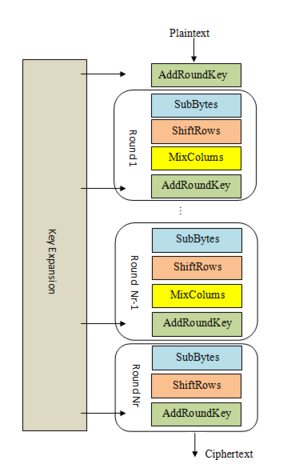
- KeyExpansion or Key Schedule
From the 128 bit key, 11 separate 128 bit “round keys” are derived: one to be used in each AddRoundKey step.
- Initial key addition
AddRoundKey - the bytes of the first round key are XOR’d with the bytes of the state.
- Round - this phase is looped 10 times, for 9 main rounds plus one “final round”
a) SubBytes - each byte of the state is substituted for a different byte according to a lookup table (“S-box”).
b) ShiftRows - the last three rows of the state matrix are transposed—shifted over a column or two or three.
c) MixColumns - matrix multiplication is performed on the columns of the state, combining the four bytes in each column. This is skipped in the final round.
d) AddRoundKey - the bytes of the current round key are XOR’d with the bytes of the state.
Included is a bytes2matrix function for converting our initial plaintext block into a state matrix. Write a matrix2bytes function to turn that matrix back into bytes, and submit the resulting plaintext as the flag.
Analyze
这题我会!
补全 matrix2bytes(),直接用 sum() 把矩阵压缩成一维列表,然后转字节输出。
补全函数的题比自己写代码的简单多了(bushi
Code
def bytes2matrix(text): |
SumUp
# function |
Round Keys
Description
We’re going to skip over the finer details of the KeyExpansion phase for now. The main point is that it takes in our 16 byte key and produces 11 4x4 matrices called “round keys” derived from our initial key. These round keys allow AES to get extra mileage out of the single key that we provided.
The initial key addition phase, which is next, has a single AddRoundKey step. The AddRoundKey step is straightforward: it XORs the current state with the current round key.
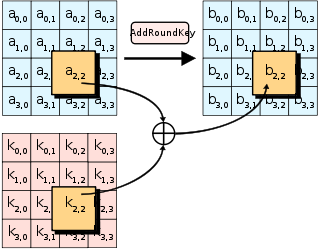
AddRoundKey also occurs as the final step of each round. AddRoundKey is what makes AES a “keyed permutation” rather than just a permutation. It’s the only part of AES where the key is mixed into the state, but is crucial for determining the permutation that occurs.
As you’ve seen in previous challenges, XOR is an easily invertible operation if you know the key, but tough to undo if you don’t. Now imagine trying to recover plaintext which has been XOR’d with 11 different keys, and heavily jumbled between each XOR operation with a series of substitution and transposition ciphers. That’s kinda what AES does! And we’ll see just how effective the jumbling is in the next few challenges.
Complete the add_round_key function, then use the matrix2bytes function to get your next flag.
Analyze
遇到异或就搬 pwn.xor()!
明文经过了 11 个不同的密钥进行异或,再异或回去就可以得到原文。
返回异或值就 ok。
感觉异或还是蛮有意思的。
Code
from pwn import xor |
Confusion through Substitution
Description
The first step of each AES round is SubBytes. This involves taking each byte of the state matrix and substituting it for a different byte in a preset 16x16 lookup table. The lookup table is called a “Substitution box” or “S-box” for short, and can be perplexing at first sight. Let’s break it down.
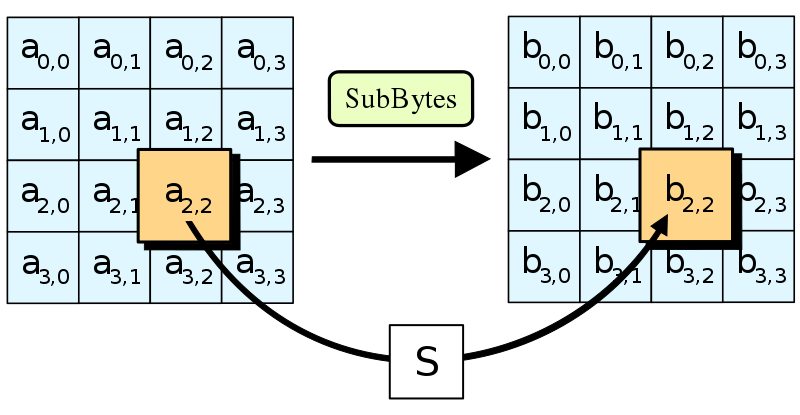
In 1945 American mathematician Claude Shannon published a groundbreaking paper on Information Theory. It identified “confusion” as an essential property of a secure cipher. “Confusion” means that the relationship between the ciphertext and the key should be as complex as possible. Given just a ciphertext, there should be no way to learn anything about the key.
If a cipher has poor confusion, it is possible to express a relationship between ciphertext, key, and plaintext as a linear function. For instance, in a Caesar cipher, ciphertext = plaintext + key. That’s an obvious relation, which is easy to reverse. More complicated linear transformations can be solved using techniques like Gaussian elimination. Even low-degree polynomials, e.g. an equation like x^4 + 51x^3 + x, can be solved efficiently using algebraic methods. However, the higher the degree of a polynomial, generally the harder it becomes to solve – it can only be approximated by a larger and larger amount of linear functions.
The main purpose of the S-box is to transform the input in a way that is resistant to being approximated by linear functions. S-boxes are aiming for high non-linearity, and while AES’s one is not perfect, it’s pretty close. The fast lookup in an S-box is a shortcut for performing a very nonlinear function on the input bytes. This function involves taking the modular inverse in the Galois field 2**8 and then applying an affine transformation which has been tweaked for maximum confusion. The simplest way to express the function is through the following high-degree polynomial:
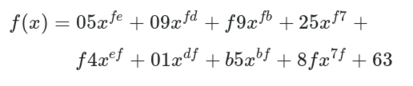
To make the S-box, the function has been calculated on all input values from 0x00 to 0xff and the outputs put in the lookup table.
Implement sub_bytes, send the state matrix through the inverse S-box and then convert it to bytes to get the flag.
Analyze
意思就是让补全 sub_bytes 函数,然后转换成字节得到 flag。
其实 state 里面的存的是它每个位置上本来的数据在查找库 sbox 中的序号,所以遍历 state,按序号取出对应的原数据,然后返回字节就好咯。
Code
# 写法一 |
SumUp
两种写法怎么说呢,第一种更简洁明了,看起来好像也更优雅。
第二种虽然搬过来了 matrix2bytes() 函数(也可以不搬函数直接一行搞定,不过读起来费劲点),看起来更繁琐,不过这种写法更不容易吃亏(在最后一题已经深刻体会过了)。所以本来是喜欢第一种写法的,做完最后一题之后还是喜欢第二种了。
(呜呜呜我也不想被钓啊,可是它解题更好用诶)。
Diffusion through Permutation
Description
We’ve seen how S-box substitution provides confusion. The other crucial property described by Shannon is “diffusion”. This relates to how every part of a cipher’s input should spread to every part of the output.
Substitution on its own creates non-linearity, however it doesn’t distribute it over the entire state. Without diffusion, the same byte in the same position would get the same transformations applied to it each round. This would allow cryptanalysts to attack each byte position in the state matrix separately. We need to alternate substitutions by scrambling the state (in an invertible way) so that substitutions applied on one byte influence all other bytes in the state. Each input into the next S-box then becomes a function of multiple bytes, meaning that with every round the algebraic complexity of the system increases enormously.
An ideal amount of diffusion causes a change of one bit in the plaintext to lead to a change in statistically half the bits of the ciphertext. This desirable outcome is called the Avalanche effect.
The ShiftRows and MixColumns steps combine to achieve this. They work together to ensure every byte affects every other byte in the state within just two rounds.
ShiftRows is the most simple transformation in AES. It keeps the first row of the state matrix the same. The second row is shifted over one column to the left, wrapping around. The third row is shifted two columns, the fourth row by three. Wikipedia puts it nicely: “the importance of this step is to avoid the columns being encrypted independently, in which case AES degenerates into four independent block ciphers.”
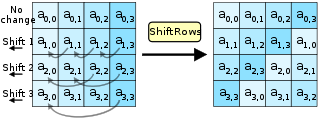
MixColumns is more complex. It performs Matrix multiplication in Rijndael’s Galois field between the columns of the state matrix and a preset matrix. Each single byte of each column therefore affects all the bytes of the resulting column. The implementation details are nuanced; this page and Wikipedia do a good job of covering them.
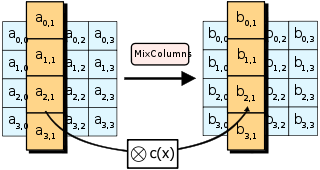
We’ve provided code to perform MixColumns and the forward ShiftRows operation. After implementing inv_shift_rows, take the state, run inv_mix_columns on it, then inv_shift_rows, convert to bytes and you will have your flag.
Analyze
首先是补全 inv_shift_rows(),参考 shift_rows(),发现是给第 n 行向左移动 n 个单位 ,那 inv_shift_rows 就给第 n 行向右移动 n 个单位。
然后根据 description 依次运行 inv_mix_columns(state) inv_shift_rows(state),然后把前面用过的矩阵转字节的函数 matrix2bytes() 搬过来,输出一下。
Code
def inv_shift_rows(s): |
Bringing It All Together
Description
Apart from the KeyExpansion phase, we’ve sketched out all the components of AES. We’ve shown how SubBytes provides confusion and ShiftRows and MixColumns provide diffusion, and how these two properties work together to repeatedly circulate non-linear transformations over the state. Finally, AddRoundKey seeds the key into this substitution-permutation network, making the cipher a keyed permutation.
Decryption involves performing the steps described in the “Structure of AES” challenge in reverse, applying the inverse operations. Note that the KeyExpansion still needs to be run first, and the round keys will be used in reverse order. AddRoundKey and its inverse are identical as XOR has the self-inverse property.
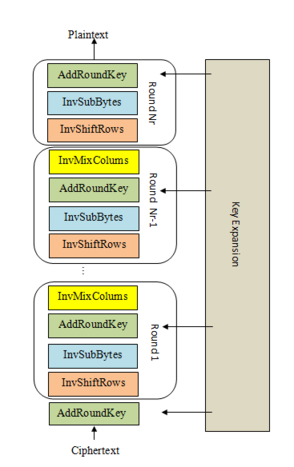
We’ve provided the key expansion code, and ciphertext that’s been properly encrypted by AES-128. Copy in all the building blocks you’ve coded so far, and complete the decrypt function that implements the steps shown in the diagram. The decrypted plaintext is the flag.
Yes, you can cheat on this challenge, but where’s the fun in that?
The code used in these exercises has been taken from Bo Zhu’s super simple Python AES implementation, so we’ve reproduced the license here.
Analyze
这题最头疼了,开始没明白到底要啥,看了半天发现是要补全好几处代码,而且给的 .py 文件还各种报错,很烦就是。
后面发现这是 AES 基础的最后一道相当于总结的题,就直接把前面几道题用到的函数和矩阵啥的全粘过来了,然后看了看有注释但没代码的地方,几乎是把前几个文件的代码拼到一起咯。然后基本就是一个完整的 AES。
还有,前面有一道题提到用了 pwn 库的 xor() 函数,现在想给自己埋咯。
最后代码一直报错,看了看日志,手写了一下 xor,居然就很顺利了?
把 pwn 库埋咯!(再次
(因为这题需要自己写的代码分布比较零散,找起来也比较麻烦,所以干脆把全部代码贴上来。)
Code
N_ROUNDS = 10 |



