网安数基复习

Part2

1. Bloom过滤器的设计，查询错误率估计

符号	含义
k	散列函数的数目
m	位向量的长度
n	集合中元素的个数

对于集合 $S={x_1,x_2,…,x_n}$ 中的⼀个元素而言，通过散列函数映射到位向量上，其某⼀位置被置 1 的概率是 $\frac{1}{m}$，为 0 的概率是 $1-\frac{1}{m}$，在将集合内所有元素通过 $k$ 个散列函数映射到向量上之后，某⼀位仍然是 0 的概率是

$P_{0}=(1-\frac{1}{m})^{kn}=[(1-\frac{1}{m})^{-m}]^{-\frac{kn}{m}}\approx e^{-\frac{kn}{m}}$

每次散列函数都刚好选中1的区域的概率，即 Bloom 的帧数误判率（false positive rate）$P$ 为

$P=(1-P_{0})^{k}=(1-e^{-\frac{kn}{m}})^{k}$

特性：
- ⼀个元素如果判断结果为存在的时候元素不⼀定存在，但是判断结果为不存在的时候则⼀定不存在。
- 布隆过滤器可以添加元素，但是不能删除元素。因为删掉元素会导致误判率增加。
优点：
- 相比于其它的数据结构，布隆过滤器在空间和时间方面都有巨大的优势。布隆过滤器存储空间和插⼊/查询时间都是常数 O(K)，另外，散列函数相互之间没有关系，方便由硬件并行实现。布隆过滤器不需要存储元素本身，在某些对保密要求非常严格的场合有优势。

2. 集合近似相等的判断 Simhash 相似哈希算法，分布之间的距离度量

集合相等的判断：

对集合中的元素一一比较，时间复杂度 $O(n^2)$
将两个集合的元素分别排序，然后顺序比较，时间复杂度 $O(n\log n)$
计算两个集合的信息指纹，直接比较，
$S={e_{1},e_{2},..,e_{n}}$ $FP(S)=FP(e_{1})+FP(e_{2})+...+FP(e_{n})$

如果两个集合相同，则其指纹⼀定相同；如果不同，则指纹相同的概率很小。

集合近似相等的判断 Simhash 相似哈希算法：

信息指纹：通过提取⼀个信息的特征，通常是⼀组词或者⼀组词+权重，然后根据这组词调⽤特别的算法（例如 MD5 算法），将之转化为⼀组代码，这组代码就是标识这段信息的指纹。

假设⼀个网页有若⼲词：$t_1,t_2,…,t_8$，每个词的权重分布为：$w_1,w_2,…,w_8$，每个词哈希值指纹为 8bit，如

$Hash(t_1)=10100110$。

Step1. 扩展：将 8 位的⼆进制的指纹扩展成 8 个实数 $r_1,r_2,…,r_8$，根据 1 加 0 减的规则，做相应的权重操作。然后遍历第⼆个词，操作的过程相同。例如， $Hash(t_1)=10100110$。
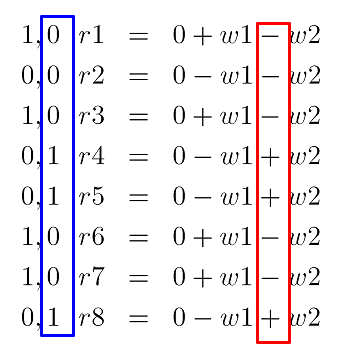
Step 2. 收缩：将最后的由权重值计算得到的网页总哈希值。如果某个位的值大于 0，则此位置上的值置 1，否则置 0。

如果 2 个网页相同，则相似哈希值必定相同。两个网页的相似哈希相差越小，两个网页的相似性越⾼。

分布之间的距离度量：

Q：两个分布 p 和 q 之间的距离有多大？

KL 散度：KL 散度可以⽤于描述两个分布之间的距离，假设 $p(x)$ 与 $q(x)$ 是随机变量 $X$ 的分布，则其 KL 散度为
$D(p||q)=\int_{-∞}^{+∞}p(x)log\frac{p(x)}{q(x)}dx$
离散情况下
$D(p||q)=\sum_{i=1}^{n}p(x)log\frac{p(x)}{q(x)}dx$

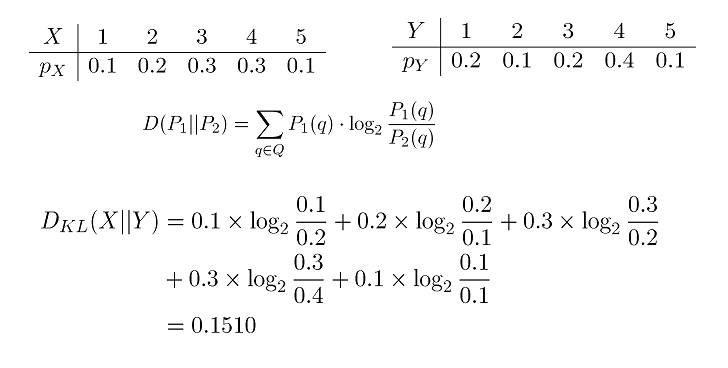
3. 贝叶斯公式，随机变量参数的最大似然估计

贝叶斯公式： 一种可以利⽤先验概率计算后验概率的方法。

$P(B|A)=\frac{P(A|B)P(B)}{P(A)}$

最大似然估计： 通过数据估计未知参数 $θ$

基本思想：给定样本取值后，该样本最有可能来⾃参数 $θ$ 为何值的总体。⼀般步骤：
- 写出似然函数
  $L(θ_{1},θ_{2},...,θ_{n})=\begin{cases}\prod_{i=1}^{n}p(x_i;θ_{1},θ_{2},...,θ_{n})\\\prod_{i=1}^{n}f(x_i;θ_{1},θ_{2},...,θ_{n}) \end{cases}$
- 对似然函数取对数，得 $\ln L(θ)$
- 两边同时求导数，得 $\frac{d\ln L(θ)}{dθ}$
- 令导数等于 0 解出似然⽅程，（$\frac{d\ln L(θ)}{dθ}=0$）

4. 朴素贝叶斯分类方法

贝叶斯分类器是⼀个统计分类器。能够预测类别所属的概率。

设 X 是类标号未知的数据样本。设 H 为某种假定，如数据样本 X 属于某特定的类 C。对于分类问题，我们希望确定 $P(H|X)$，即给定观测数据样本 X，假定 H 成⽴的概率。贝叶斯定理给出了计算 $P(H|X)$ 的⽅法:

$P(H|X)=\frac{P(X|H)P(H)}{P(X)}$

$P(H)$ 是先验概率，或称 H 的先验概率。 $P(X|H)$ 代表假设 H 成⽴的情况下，观察到 X 的概率。
$P(H|X)$ 是后验概率，或称条件 X 下 H 的后验概率。

5. 信息熵，信息增益，简单的决策树的构建方法

信息熵： 解决了对信息的量化度量问题。

信息增益（Information Gain）：

We want to determine which attribute in a given set of training feature vectors is most useful for discriminating between the classes to be learned. Information gain tells us how important a given attribute of the feature vectors is. We will use it to decide the ordering of attributes in the nodes of a decision tree.

Entropy $H(X)$ of a random variable $X$

$H(X)=-\sum_{i=1}^{n}p(x_i)\log_{2}{p(x_i)}$

Specific conditional entropy（条件熵）$H(X|Y=v)$ of $X$ given $Y=v$

$H(X|Y=v)=H(X)=-\sum_{i=1}^{n}p(x_i|Y=v)\log_{2}{p(x_i|Y=v)}$

Conditional entropy $H(X|Y=v)$ of $X$ given $Y$

$H(X|Y)=\sum_{v∈values(Y)}P(Y=v)H(X|Y=v)$

Mutual information (aka Information Gain) of $X$ and $Y$

$I(X,Y)=H(X)-H(X|Y)=H(Y)-H(Y|X)$

简单的决策树的构建⽅法：

node=root of decision tree

Main loop:

A <- the “best” decision attribute for the next node.
Assign A as decision attribute for node.
For each value of A, create a new descendant of node.
Sort training examples to leaf nodes.
If training examples are perfectly classified, stop. Else, recurse over new leaf nodes.

6. 差分隐私的定义，后加工不变性、串行合成性、并行合成性的证明

差分隐私（Differential privacy）的定义：

后加工不变性（Posting-processing）：

串行合成性（Sequential composition）：

并行合成性（Parallel Composition）：

7. 差分隐私的 Laplace机制；本地差分隐私中的随机响应技术；差分隐私的Laplace机制：

全局敏感度：

$A(x)=f(x)+Lap(\frac{GS_f}{∊})\ is\ ∊-DP$

Laplace 分布：

$f(x|\mu,b)=\frac{1}{2b}e^{-\frac{|x-\mu|}{b}}$

为了达到 ∊-DP，可以给输出结果加上⼀个噪⾳进⾏掩盖和混淆：

$f'(D)=f(D)+X$

其中 $X$ 是需要添加的噪声，添加噪声后的结果应满⾜：

$\frac{P[f'(D)=t]}{P[f'(D')=t]}=\frac{P[f(D)+X=t]}{P[f(D')+X=t]}=\frac{P[X=t-f(D)]}{P[X=t-f(D')]}\leqslant e^{∊}$

令 $d=f(D)-f(D’)$，$x=t-f(D)$，

$\frac{P(X=x)}{P(X=x+d)}\leqslant e^{∊}$

如果 $X \sim Lap(b)$，

$\frac{P(Lap(b)=x)}{P(Lap(b)=x+d)}=\frac{\frac{1}{2b}e^{\frac{|x|}{b}}}{\frac{1}{2b}e^{\frac{|x+d|}{b}}}=e^{\frac{|x+d|-|x|}{b}} \leqslant e^{\frac{d}{b}} \leqslant e^{\frac{\Delta f}{b}}$

要想让上式小于 $e^∊$ ，只需要让 $\frac{\Delta f}{b}=∊$，即 $\frac{\Delta f}{∊}=b$，因此加入噪声 $Lap(b)=Lap(\frac{\Delta f}{∊})$。

本地差分隐私中的随机响应技术：

本地差分隐私：认为第三方是不可信的，所以本地差分隐私保护的是用户上传数据到第三方的过程，差分隐私机制运行在各个用户的本地。

随机响应技术（randomized response）：

假设有n个⽤户，其中艾滋病患者的⽐例为π，我们希望对π进⾏统计。于是对⽬标⽤户发起问卷调查：“你是否为艾滋病患者？”显然，如果直接获得⽤户的相应数据进⾏统计，⼀旦数据泄露，那么⽤户隐私随即泄露。因此，我们假设存在⼀枚⾮均匀的硬币，其正⾯向上的概率为p，反⾯向上的概率为1-p。抛出该硬币，若正⾯向上，则回答真实答案，反⾯向上，则回答相反的答案。

显然，$\Pr[X_i=是]=\pi p+(1-\pi)(1-p)$，$\Pr[X_i=否]=(1-\pi)p+\pi(1-p)$。设回答 “是” 的人数为 n1，回答 “否” 的人数为 n2。⽤极大似然估计（Max Likehood Estimation）对 $\pi$ 统计结果进行估计。首先构建似然函数：

$L(\pi)=[\pi p+(1-\pi)(1-p)]^{n_1}[(1-\pi)p+\pi(1-p)]^{n-n_1}$

可以求出 $\pi$ 的极大似然估计，并验证是 $\pi$ 的无偏估计，由此可以得到患病的总人数。

8. 简单的传染病传播模型 SI；免疫方法；网络中节点的度中心性度量

简单的传染病传播模型 SI：

SI : lSusceptible, and once you catch the disease, you remain infectious for the rest of your life.

假设条件：

人群分为易感染者（Susceptible）和已感染者（Infective）两类，简称健康者和病人。t 时刻这两类人在总人数中所占的比例分别记为 $s(t)$ 和 $i(t)$，初始时刻（$t = 0$）病人的比例为 $i_0$。
在疾病传播期内所考察地区的总人数 N 不变，既不考虑生死，也不考虑迁移，时间以天为计量单位。
每个病人每天有效接触的平均人数是常数 l，l 称为日接触率。当病人与健康者有效接触时，使健康者受感染变为病人。
$i(t)=\frac{1}{1+(\frac{1}{i_0})e^{-\lambda t}}$

当 $t\to \infty$ 时，$i \to 1$，即所有人终将被传染变为病人，显然不符合实际情况。其原因是模型中没有考虑到病人可以治愈，人群中的健康者只能变成病人，病人不会再变成健康者。

这个模型在传染病流⾏的前期是可用的，可用它来预报传染病高潮的到来：

$t_m=\lambda^{-1}\ln(\frac{1}{i_0}-1)$

免疫方法/免疫策略：

Pastor-Satorras 等的研究表明：在资源有限的情况下，优先保护节点度数比较大的节点比随机选择节点进行保护效果要好得多

随机免疫：随机免疫是在网络中随机抽取一部分节点进行免疫。研究表明，采取这种策略的话，需要对网络中几乎所有的节点都进行免疫才能保证最终消灭传染病。
选择免疫：选择免疫是在网络中抽取度最大的节点进行免疫。针对 BA 模型，采取选择免疫策略，即使有效传播率变化，也可以只免疫很小一部分节点就保证消灭传染病。
熟人免疫：熟人免疫采取的是随机抽取⼀部分节点，然后对每个节点随机选⼀个与之相连的“邻居”节点来进行免疫。

由于在无尺度网络中，度大的节点可以与非常多的节点相连，因此选择“邻居”免疫的话，碰到度大节点的概率会比碰到度小节点的概率大得多。所以熟人免疫要比随机免疫有效得多，只略差于选择免疫。

网络中节点的度中心性度量：

直观上看，⼀个节点的度越大就意味着这个节点在某种意义上越 “重要”（“能力大”）。

度(degree)：节点 i 的度 ki 定义为与该节点连接的其他节点的数⽬。

网络的平均度：网络中所有节点的度和的平均值。

度分布函数 $p(k)$：随机选定节点的度为 k 的概率。

9. 齐次 poisson 点过程的定义；在 HPPP 中，相邻节点之间的距离分布；Campbel 定理的应用，掌握计算齐次 poisson 点过程中，空间点的某函数的和的期望的计算方法。